
"What are we doing to help kids achieve?"
The concept of the mole has always been a challenging topic for myself and my students. The challenge comes in part when we try to imagine 6.02 x 1023 of anything. Another challenge for some students is the math and theory behind this number and concept.
Years ago I started using and tweaking an activity found in an old version of Zumdahl’s “World of Chemistry” textbook. Students start with four different type of beans. They count 50 of each bean and find the mass of each set. Students use the mass of 50 of the smallest bean and divide all of the other masses by this number. They then get the “relative” masses compared to the smallest bean. Some sample data is shown in Table 1.
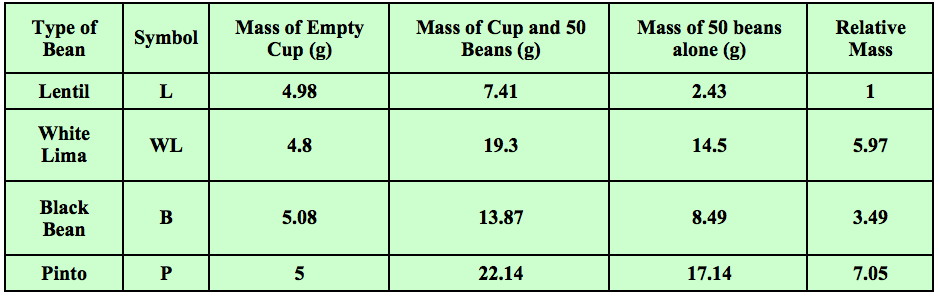
Table 1 - Students find the masses and relative masses of sets of 50 beans of four different types.
In the above example, 50 lentils had a mass of 2.43 grams. Fifty white limas had a mass of 14.5 grams. 14.5 grams divided by 2.43 grams is 5.97. This is the “relative” mass of the white limas as compared to the lentils. The relative masses of the other beans were calculated in the same manner. They were all compared to the lentils. Students had just done an activity prior to this in which the examined data that showed that as long as you are comparing the same number of items, you are also comparing the same mass ratios.
Here is where I “tweaked” the published activity. My students were instructed to carefully place on a scale for each bean an amount of beans that would get them to the relative mass for that bean. As an example, they had to place an amount of lentils on the scale to get to one gram. They then had to place white limas on the scale to get to 5.97 grams. They would repeat this for the pintos and black beans. Now the emphasis was on a simple question. Will the number of beans in the end for each relative mass in grams (which by the way was given the unit "a pot") be the same or different for all the beans? You can see some sample data in Table 2.

Table 2 - Finding the number of beans with a mass equal to the relative mass of each type of bean.
In the end, students saw that the same number of beans would provide the same ratio of masses of beans (Table 1). The opposite is also true. The relative mass of the beans in grams would provide the same numbers of beans which is about 20 (Data Table 2). If they did not want to count out a bunch of beans, they could just count by using the relative masses and a scale. This provided a great model for the mole. It took awhile but it was an easy transition from the relative masses of atoms and amu's to molar mass and the mole.
Moles seem to be tough for students and teachers. Do you have a great mole activity? Please share….would love to take a look.
NGSS
Students who demonstrate understanding can use mathematical representations to support the claim that atoms, and therefore mass, are conserved during a chemical reaction.
*More information about all DCI for HS-PS1 can be found at https://www.nextgenscience.org/dci-arrangement/hs-ps1-matter-and-its-interactions and further resources at https://www.nextgenscience.org.
Students who demonstrate understanding can use mathematical representations to support the claim that atoms, and therefore mass, are conserved during a chemical reaction.
Assessment does not include complex chemical reactions.
Emphasis is on using mathematical ideas to communicate the proportional relationships between masses of atoms in the reactants and the products, and the translation of these relationships to the macroscopic scale using the mole as the conversion from the atomic to the macroscopic scale. Emphasis is on assessing students’ use of mathematical thinking and not on memorization and rote application of problem - solving techniques.

All comments must abide by the ChemEd X Comment Policy, are subject to review, and may be edited. Please allow one business day for your comment to be posted, if it is accepted.
Comments 26
Excellent Anchor Activity!
Hi Chad,
I do a similar activity with beans in my classes, though I do not have the relative mass aspect included. I am going to add this to my version right now! I based my activity on this activity from AACT.
It provides a great anchor for the rest of the unit as students continue to try to understand moles and relative masses. The number of times I say something similar to "silver atoms are like kidney beans, and hydrogen atoms are like lentils." I highly recommend activities such as this as an intro to the mole for any chemistry class.
Thanks!
Kaleb - Thanks for sharing. I like the AACT activity better. It has the questions phrased better than the ones that I have. Might have to use this for next year. I totally agree that it is a great anchoring activity. Thanks again.
I've found students struggle
I've found students struggle with the relative mass idea when it comes to molar mass. I'd like to try this idea! Would you be willing to share the writeup you use with students?
No problem...
I'll try to post it this weekend.
Mole Conversions
In my teaching of chemistry, I used to provide students with a "Mole Conversion Chart" to assist them in making conversions into and out of moles with number of particles, mass and gas volume.
Conversion charts
Hi John,
I have used something similar to the chart you shared as well. While I recognize that charts like this can help students to arrive at mathematically correct answers I have found students can rely on these "tricks" so much they don't actually learn the chemical concepts behind the mole or molar relationships. They can simply plug numbers into an alogrithm and out pops an answer. I have adjusted my instruction to encourage students to build a strong conceptual understanding of these fundamentals. Using tools like BCA tables and "for every statements" my students understand the mole and stoichiometry in a way they never did when I provided them with a mole map. I encourage you to check out the two blogs I linked here :)
Conversion charts, mole maps, etc.
I also used a "mole map" of sorts for several years but have avoided it the last couple of years as I try to move away from tricks towards a greater conceptual understanding. I'm excited about the progress I've made with the mole, and want to check out Chad's lab he references in his comment. Using proportions and "for every" statements has helped tremendously, so has using the lab activity described in this post! My students have a much better understanding of the mole than they ever did (and my old students could get the right numbers!).
Of course, students find such aids on the internet and from tutors and if it helps them get the write mathematical answer then thats one piece of the puzzle, but if they don't understand why they're doing the math they're doing then they don't yet have a complete understanding. For students who are over-reliant on these types of aids and claim "I can only do the problems with my mole map" then I work with them to help build in the conceptual framework and then challenge them to make their own graphic organizer that incorporates some of the conceptual aspects.
Ah, the mole. What a wonderfuly useful concept and one that gives our students some of the biggest troubles.
I like both ideas...
First, I like BCA tables and "for every statements". I have to say... I have kids with a super wide range of abilities. In an ideal world I would love to do BCA tables and have kids internalize "for every statements". For some kids, I am just not able to get them there. They can do the mole map. Part of it is that I have to pick and choose my battles. Honestly, I constantly loose sleep over it....that's why I write blogs and shamelessly steal ideas from anyone I can. Not to throw another wrench in the system but I did Argument Driven Inquiry for the first time on, of all things, moles. Funny thing happened...some of the kids solved for moles in ways I have never seen in 20 years of teaching...but they got the correct answer. Highest test scores ever in this topic with this particular group of kids. Here is an idea...maybe it might be interesting to offer methods of solving problems but to utlimately let them discover the method that works for them. Just something to toss up the flag pole....still trying to figure out this teaching thing....
"Their Own Way"
I think letting studetns figure out their own way is huge. I prefer proportions when I set up mole calculations, and most of my students will use proportions. I will happily expand upon the superiority of proportions to dimensional analysis if anyone is curious or unfamiliar.
But the point is that some students will use dimensional analysis, some will use the algebraic relationshiop n = m/M, and those who really "get it" intuitively will just multiply and divide as appropriate. Of course, all have to show work and label all of their numbers. You do not have to show the work like I do, but you do need to show your work and label!
This variation was hard for me to get used to, but it is really beneficial for students. What is important is that they understand the material. Of course, some students "need" a nice structure, and if that is the case then I tell them to follow me! :)
Another factor to consider...
I agree with what you are saying. Another factor not mentioned is the level and abilities of students. I have had students who have some really serious struggles with the simplest math. There could be a student next to them who can do it without a problem. I would like for them to do it the best way possible but I also have 20 other kids in the room and I have to pick and choose. I have been pleasantly surprised lately that when I have given them some time to problem solve they do it in ways that surprise me....might be a future blog post here....
If you can get the right answer...
I've been teaching on mole conversions and dimensional analysis recently and encountered this issue. In fact, I just had a student make that exact argument in a snarky note on the bottom of a quiz. It shouldn't matter HOW she got the answer as long as she got the right answer. I find a few problems with that argument. First of all, the student got ALL the problems wrong. She didn't get a single answer correct, so doing it her own way obviously doesn't work. Second, if the process doesn't matter than taken to a logical end, copying the answer from your neighbor's paper is an option. Third, and most importantly, the chemistry isn't the point. As I told a student the other day who asked the dreaded "when am I ever going to use this" question. Learning dimensional analysis is like weightlifting. We're training the brain to solve problems. It is important to learn new ways to solve problems. So even if you could solve that problem another way you already know how to do, learn dimensional analysis builds our ability to solve problems in new and novel ways.
Difficult to give up old tools
I was once steadfast in my traditional methods of teaching of stoichiometry. Dimensional analysis/factor label method made sense to me as a student and a teacher. If you set up the problem using the roadmap, units cross out nicely and you get the correct answer. The problem was that every year I would have students that just could not make sense of that roadmap. No matter what I did, they focused on memorization of the steps rather than on what was happening in the reaction. Some would fail the chapter test miserably (not just fail...but fail with a rock bottom score). I did try to allow my students to use their own method, but found that i was struggling to help students that were not coming up with the correct answers. I had to first wade through the set up of their problems to figure out where they were going wrong. I found a small measure of success when I worked with students to come up with the roadmap themselves, but I was still not reaching all of my students. When I finally was introduced to BCA tables, it took a leap of faith on my part to use them with my students. It is not easy to give up those old tools that we used as students ourselves. I found that the processes really helped to level the playing field. The students that would have been successful using the roadmap, found the BCA tables to be so easy that they didn't want to waste their time setting up the tables. The students that would have probably struggled with memorizing the roadmap found the tables very useful. Most importantly, my stoichiometry assessments became much more conceptually based. They had not just memorized the steps, but they recognized the ratios involved in balanced equations and reactions. Even though the difficulty of my stoichiometry assessment questions increased, the average scores went up drastically. As if that was not enough, i was really convinced the following year when the students that moved on to AP chemistry moved through an even higher level of stoichiometry problems and other topics (equilibrium is just one of those) quicker and more confidently than ever.
Erica Adams-Posthuma offered links in her comments above that I hope our readers will read with an open mind. I am hoping that our Modeling InstructionTM residents will continue to offer information on how to transition to methods that help our students build deeper conceptual understanding along with problem solving skills that will serve them well after they leave the classroom.
It is through discussions like these that we can reflect on our practices, support each other on our journey in this important field of work, and grow as teachers. I only wish there was a platform like this earlier in my career.
Best Regards,
Deanna
The Nursing Math Quiz
At my daughter's univesity all nursing students had to pass the Math Quiz with a 100% (25/25) at the end of every semester (8 times over 4 years), or they had to take it again until they passed it. It was almost exclusively conversion factors: what dose for what weight patient, how much time between doses, etc...
The first time she failed with a 92% (23/25), an A in her mind. She groused about this until I asked her, "So, Honey Bear, which two out of 25 people are you willing to kill because you overdosed them by a factor of three or they did not get a high enough dose by a factor of three?" She never dropped another point.
Food for thought...
Here are a couple of thoughts. First, I get your point. If the only students I had were nursing students and I knew for sure they were all facing life and death decisions I would probably look at things differently. This is not the case. It seems from the comments above that many people have different ideas and experiences. Here is what I would like to suggest....what does the majority of the research say about how students learn best?
Here is why I like ChemEdXchange. The research shows convincingly that when teachers work together to find ways to help kids, students do better (as opposed to working alone in our separate worlds). What if we apply the research question to other topics? How about moles and stoichiometry? What does the research say is best for most of the students? I can't always be a teacher and a chemical education researcher at the same time. I do know that Johnstones triangle has been pretty well established through research and I think that BCA tables would be favored more than using conversion factors. In an ideal world I would like to have all of my students have a firm understanding of the macroscale, the particulate and the symbolic. However....I also have to deal with reality. Also, to be honest, do all nurses have to have a complete understanding of this triangle to dispense medicine? Again....tough questions. Ideally, I would want students and caregivers to have a firm understanding on many levels of the chemistry that effects their life. I can't always meet that standard or know the best way to help students get there but that is why I see this forum as so valuble...it helps me to keep trying. I hope it helps us all. Thanks for your thoughts and comments. In the end, it makes me a better teacher and helps my students.
It is a (non-fiction) story. Some would like a train of thought
I am not a high school teacher, so perhaps my being in this discussion is misplaced, but here it goes.
First, with respect to my daughter, this is a story: a non-fiction one, but a story nonetheless. Any story will speak to some people, and not to others. It clearly did not speak to Chad Hustings as he seems to think that it only applies to health care professionals. I teach few who are interested in health care as a profession, but many see the larger point. So, if a story does not work for you, do not use it, but do not needlessly narrow its scope.
Second, I am beginning to appreciate the difficulties many have in trying to teach the one-step problems to those who have difficulty with these. However, it takes a highly skilled practitioner to take proportions beyond one-step, and the only reliable method is to show units and use them. I am not saying that instructors that use proportions do not emphasize that no physical property is a pure number (that is a numerical representation without units), I am just saying that using unitless numbers is how many students remember the instruction, and how they use them in problems. Among common errors that occur occur two are, 1) when one gets confused and get the inverse of a value, and 2) that many intensive properties, such as density and concentration, are “hidden conversion factors”. A prime example is teaching solution stoichiometry where treating concentration without revealing the hidden units (for example, M = mol/L) quickly makes the problem unmanageable.
Finally, related to the second point, dimensional analysis is inherently expandable to include a train of thought: proportions and Johnstone’s triangle do not. It is what is called “an elegant solution”. An elegant solution solves the problem that you have in front of you, and can be used to solve ones you had not initially considered or even imagined. I have been the recipient of many people trained to think in one-step problems, and 1) are bereft of the tools to expand the train of thought, and 2) are locked into one-step problems. They are resistant to change because “one-step” has always been enough before.
Both identifying numbers with physical reality, and connected, reasoned thought are laid out in their barest form in dimensional analysis. We teach things that do not show up on a multiple choice exam, and these two big-picture concepts are useful to any thoughtful citizen and any learner in any discipline inside or outside of school.
Thank you for your input.
Thank you for your input. I really appreciate your ideas about dimensional analysis. I do agree that it can lead to other ideas. For instance, I remember being stuck in college on my first physics exam. I had no idea how to solve a particular problem. Dimensional analysis helped me arrive at the correct answer. I completely agree that what you said is correct about identifying numbers with a physical relity and connected, reasoned thought are laid out in the barest form in dimensional analysis. I struggle with students who just want to use it to "plug and chug" to get the answer and totally miss the physical reality when I probe a bit further. Maybe I am not teaching it correctly?
Also, I certainly meant no disrespect to your daughter or any nursing students. I still would like to look at what the research says works best for most students. If I am going to teach a science class and I want my students to base arguments and decisions on data, I would like to try and do the same. After all, instead of believing me, why not examine data from possibly hundreds of students and classrooms in an attempt to get a better handle on a difficult topic? The struggle for me is being able to sift through the chemical education data, teach, grade and do labs all at once.
I would enjoy learning more about your journey. Would you consider talking about or posting some of your lessons, ideas or demonstrations on this forum? Again....still trying to find better ways to help students...thanks again for you time and thought...
Teaching Moles through Beans
Dear Prof. Chad,
Further to my earlier observations, I would like to add the following.
The constant in the last colomn of Table 2, depends on the bean chosen as reference (you have taken Lentil).
What the last colomn says is this: Beans per gram x Relative mass in grams = Constant = Pot.
The value of the 'pot' depends on the reference bean chosen. The constant represents the number of reference beans per gram. The value of Pot = 20.58, if we choose L as the reference bean. The value of Pot = 3.45, if we choose WL as the reference bean, 5.89 if we take BB as the reference bean and so on.
In order to relate the concept of mole, we must connect it (take it) from bean to atom or molecule and the relative mass of bean to relative atomic (or molar) mass and the constant to Avogadro constant.
Teaching Moles through Beans
I've been teaching on mole conversions and dimensional analysis recently and encountered this issue. In fact, I just had a student make that exact argument in a snarky note on the bottom of a quiz. It shouldn't matter HOW she got the answer as long as she got the right answer.
Can it be applied in multiple situations?
I agree with Joseph that an apporach is best when it can function in multiple situations and not be limited to just solving one type of question. Even better when you can build on it later to teach a future concept. In the case of dimensional analysis I've always had a mixed view of it since the multiple step calculation needed to convert something like cm to feet always gave my students problems. These were kids that had difficulty isolating a variable so having them do a multi-step DA didnt end well. I chose not to make metric to US unit conversions a focus early in my career but I didnt want to make the art of calculating something like density to turn into a discussion about a pyramid and which letter a student should cover in order to answer a question. This would not help them with future concepts and gave them a one trick pony that would provide no use for them outside of my class. Add to that the need to at least do a T-chart for stochiometry and I was forced to avoid the simple formula approach, but had to do it in a way that would work with my kids. My solution has been to do all DA questions one step at a time. That meant that going from grams to mL of water required students to make a T-chart with 1 gram on the bottom and 1ml on top with unit cancellations and it meant going from grams of He to atoms required two t-charts. One for going to moles and another going from moles to liters. Gone were the multiple conversions written right next to each other found in books requiring students to mutliply and divide multiple numbers at one time and in was a one step at a time apporach my students were able to understand and could apply to a variety of questions Students were able to not only do multiple step conversions for the mole but could also do stoichiometry without getting lost. By embracing dimensional analysis and focusing on an apporach that would work with my students I was able to make sure my students had a skill they could use in the future and build on when a question they have never seen before pops up on a test.
The importance of standard algorithms
Chem Ed is a combination of the science of molecular behavior and the science of how the brain learns and solve problems. Late in my career, most of my reading has been on the “brain” side, where the science that is agreed-upon has expanded rapidly in the past decade.
According to the scientists who study how the brain solves problems, the fundamental rule is: Working memory (where the brain thinks and solves problems) can hold unlimited amounts of well-memorized information, but can hold on to minimal chunks (yes, they call small elements of knowledge “chunks”) of not-well-memorized information at any one time.
For students prior to grad school, trying to solve problems by general reasoning skills, or by modeling, or by “thinking like a scientist,” would be wonderful it worked, but in 2018, leading cognitive scientists are in agreement that those methods do not work. Cognitive scientists Alloway and Gathercole (2006) note that for non-recallable information,
“the capacity of working memory is limited, and the imposition of either excess storage or processing demands in the course of an on-going cognitive activity will lead to catastrophic loss of information from this temporary memory system.”
During problem solving, unless the fundamental facts and algorithms of a discipline are recallable from memory (memorized), student working memory tends to quickly overload and confusion results.
To get around the working memory limit, one method is to apply “standard algorithms.” These are stepwise procedures that limit how much information must be held in working memory at each step during processing. One example would be the standard algorithms most of us learned for multi-digit arithmetic operations such a "long division."
Cognitive experts emphasize that, though more than one algorithm can be used to solve most problems, students should be taught and master one widely-applicable standard algorithm, because learning multiple methods tends to create “interference” in the recall of algorithmic steps.
In chemistry, the standard algorithm used to solve multi-step problems in every college general chemistry and physics text is dimensional analysis. If one goal of a chemistry course is to prepare students for success in college sciences, this suggests that dimensional analysis should be taught and practiced at all introductory levels.
Activities involved in POGIL and Modeling, according to the cognitive experts, as
“problems and projects can be effective – not as vehicles for making discoveries, but as a means of practicing recently learned content and skills.” (Clark 2012)
For a short PDF summary of these recent findings, written by cognitive experts but largely jargon free, search “Putting Students on the Path to Learning – Clark 2012”
I think you will find the findings of cognitive science are consistent with your personal experience in learning and teaching chemistry.
-- rick nelson
Christmas Pageants, Behaviorism and the challenges of GenChem
I have been gratified by comments on this thread. Particularly by Rick Nelson and Chad Husting. The central issue of general chemistry instruction is state by Chad Husting in, “I struggle with students who just want to use it to "plug and chug" to get the answer and totally miss the physical reality when I probe a bit further.”. How do you create an environment where you can develop technique while not having them lose sight of what the technique is doing?
There is a certain amount of technique building necessary to put the student in a place where they are comfortable enough to go further, to what I refer to as Searching out the Why behind the What. The What (the lab technique, the conversion factor computation, the valence electron counting in creation of a Lewis structure, etc…) is necessary, but incomplete instruction.
I relate it to directing a play with unskilled performers under time constraints, perhaps a Christmas Pageant with a host of grade schoolers with one practice. You really do not have time to workshop it so they can to delve deeply into the story, determine the motivation, and have them figure out where on the stage to put the stable. You put a costume on them, tell them which side of the stage to come in, put a Post-It on the floor with their name on it, and you tell them to point at the star. However, eventually—perhaps in a later class—you need to relate their actions back to the story and its meaning.
Now relating this to the general chemistry classroom. With the unskilled purveyor of understanding connections of numbers to physical reality, one may, metaphorically, need to give them a costume (a lab, a book, a calculator …), tell them where to stand (give them clear instructions about the technique), and tell them to point at the star (work through the lab, cancel out the units, determine the number of bonds in a structure). But it is the deeper mission of the instructor to know the greater meaning, keep it in mind as one continues and not let the frustration of one performance (on stage or in an exam) narrow either their own focus or the type of techniques they use. Life has plenty of limitations—time, money, interest, motivation, ability. There is no reason to add to them.
There is plenty of behaviorism in teaching general chemistry, to put it another way. We give them safe, correct (or at least as correct as a particular model can take us) and expandable methods to use before they understand why they use them. Our student body’s knowledge and working memory is heterogeneous, sometimes immensely so. One never knows when sliding an underlying Why into the discussion of What will lock in the knowledge and provide a bit of wonder. I have to admit that I probably try slipping more of the physical connections of particular mathematical manipulations and macroscopic models into the discussion than a significant portion of my student body can digest. That which is “straying from the topic” for one student is “giving deeper insight” to another. I feel a deeper duty to the deeper insight, not that I do not feel empathy for those who would rather I stick to their topic.
Finally, excuse me for being so philosophical in a very useful and practical discussion, but despite the problems (and computations) of today, I would contend that our responsibility and joy extend beyond. After all, one cannot see the star without knowing to look to the sky.
Important discussion, but off topic of original post
I am greatly encouraged to see that Chad’s post has generated a great deal of conversation. I enjoy reading comments and seeing that our readers are engaged in what is happening at ChemEd X. However, I feel that the content of the discussion has strayed from the original topic on which Chad wrote. Therefore, I will be closing further comments on this item, except those specific to the original post.
This conversation is an important one as our community strives to improve their practice and update their curriculum to meet the standards set forth by the NGSS. For those wishing to further this discussion, I encourage you to submit a blog post or article to ChemEd X, where the discussion can continue. By specifically addressing some of these issues in a new post, the authors can reach readers who are interested in the topic. Information about how to do contribute can be found on our Contribution page.
Thank you all for your engagement. I fully expect that we will revisit this important conversation again.
Write Up/Handout For Activity??
Hi Chad,
I saw above that you said you would post your write up for this activity, but I don't see it. Did you ever post it? It sounds like a great way to introduce moles and we're trying to find a new intro activity.
Thanks!
Student Pages & Spreadsheet
Chris, thanks for your interest! Chad uploaded the documents you are interested in. When logged in, you can download them from Supporting Information. I hope this works well for you!
Deanna
Bean Lab
I was reviewing my mole unit and found a printed copy of your ChemEd Xchange post regarding the Bean Lab. I have also used the Bean Lab for many years to teach the mole and find the idea of relative mass helpful in other areas of chemistry such as empirical formula determination. I have also made improvements each year I have used it. Relative mass is a mass ratio and students struggle to interpret them and understand that units of mass are not important. I am in need of improving the idea that amu/atom and g/mol are two interpretations of the mass on the PT. You mentioned that you do a prior activity to the bean lab in which the examined data showed that as long as you are comparing the same number of items, you are also comparing the same mass ratio. I think this would really help my students and was wondering if you would be able to share it with me?
Prior Activity
Andrea - Thanks for the email. My prior activity is a POGIL activity on moles. The activity starts by comparing different amounts of eggs and calling a unit a "cluckster". The kids kind of get the numbers and then the above activity helps a bit more with their understanding. Please let me know whatever improvements you do. I am always trying to find ways to "tweak" things. Thanks again.