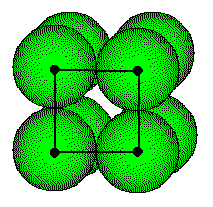
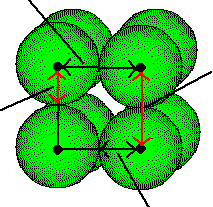
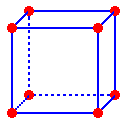
The centers of the atoms in a simple cubic are located at the lattice points and they touch half-way along the unit cell edges

The length of the unit cell, a, is equal to twice the radius of the atom or, conversely, the radius of the atom, R, is one-half the length of the unit cell edge. The radius of the metal atom can be determined by measuring the edge length of the unit cell. This is done by x-ray diffraction.

Click the links on the right to illustrate these topics, and click on the underlined text above to view a definition for x-ray diffraction.